Catalogue of variations and implementation choices for linked lists.

Introduction

Alex Stepanov mentions at some point that std::vector is just a kind of vector, there are many kinds of vector. It turns out that std::list is also just a kind of linked list, the are many kinds of linked lists.

Linked lists are dynamic-size data structures that are implemented as a chain of nodes. Each node stores a value and one or two pointers to adjacent nodes.

A list has a header (consisting of the local parts, at fixed offsets from the list object address) and the chain of nodes (the remote parts). The chain is accessed through at least one pointer in the header.

Like extent based data structures e.g. std::vector, linked lists expose a sequence of values. The differences are in terms of trade-offs for the cost of operations. Linked lists take advantage of the fixed locations of the nodes and the option to re-link pointers of existing nodes. Extent based data structures take advantage of processor/hardware pre-caching for sequential access. That’s why std::vector out-performs lists for most common scenarios.

Most of the list logic does not depend on the value, that’s why the implementation is usually generic e.g. a template parametrised by the type of the value.

There are several design choices that lead to different kinds of linked lists.

Single linked vs. Double linked

Single linked lists have a pointer to the next node.

Double linked lists have an additional pointer to the previous node.

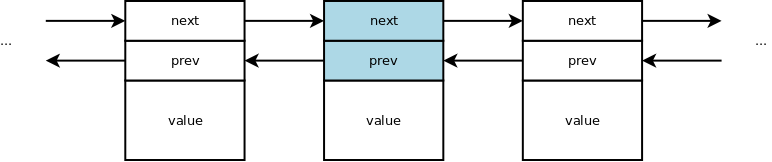
NOTE: In the diagram above the prev pointers would really point to node, not to the prev member of the node, but that more precise diagram would have made for a more difficult read.

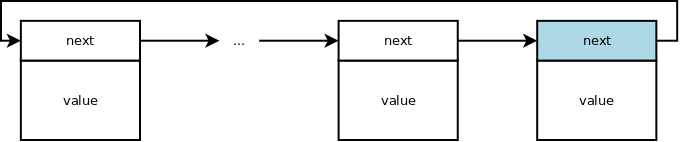
Linear vs. Circular

There are two choices for the next pointer of the tail node.

It can be nullptr, not pointing to another node. In this case the list is linear.

Or it can close the loop pointing to the node at the other end of the chain. In this case the list is circular.

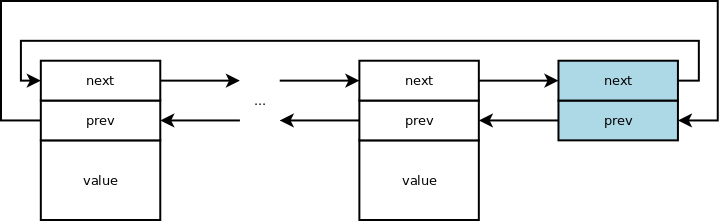
Double linked lists have the same choice for the prev pointer for the head node. A double linked list is either linear for both chains or circular for both chains.

Header - minimalistic

A minimalistic header can have just one pointer. That’s useful for large number of lists, many of which are empty.

The minimalistic header can have a pointer to the head (e.g. a linear single linked list).

Or the minimalistic header can have a pointer to the tail, This can work for circular lists, by providing access to the head as well in a constant number of steps regardless of the length of the list.

Alternatively the header can be larger than just a pointer.

Iterators - minimalistic

A minimalistic list iterator can be simply a pointer to a node with simple logic to advance by one position by following next (or prev).

Or they can be larger (for advantages elsewhere).

List size

The list can store its size in the header and adjust it when values get inserted or removed.

Or it can dispense with storing it. This leads to a smaller header. It requires O(N) to calculate the list size (traversing and counting the list nodes). This is not as bad as it sounds as more often the question is whether the list is empty or not (which can be exposed in constant time) rather than the list size.

Splicing

Splicing refer to the operation of transferring list nodes from one list to another. It can be total, when all the nodes are transferred from the source list, or partial, when a range of nodes are transferred.

NOTE: Splicing usually involves adjusting pointers of the end of the transferred range and can have constant time complexity. If the list size is cached in the header, splicing time complexity might be linear, proportional with the number of nodes transferred (to calculate the count of nodes transferred in order to update the cached size).

Operations available

All lists provide:

• constant time access to the front (the first value)
• constant time push_front
• constant time pop_front
• constant time insertion and erasure after iterator (i.e. other than the end iterator)
• some form of splicing

Typical optional operations are:

• constant time access to the back (the last value)
• constant time push_back
• constant time pop_back
• constant time insertion and erasure before (and at) iterator
• constant time partial splicing

Links from remote parts to local parts

One option is to only have links from the header (the local parts) to the nodes (the remote parts), but no links from the nodes (the remote parts) back to the header.

The other option is to allow links from the nodes (the remote parts) back to the header (the local parts). This makes some operations a bit more complex (e.g. move constructor and assignment need to also adjust the relevant pointers to point to the new header).

Dummy node

Dummy nodes refer to nodes that just have the linking pointers, but not the value (e.g. they are effectively reinterpret_casted to a node), with the goal of simplifying code in some cases.

In the example below a dummy node is inserted between the node for the front (the node of the first value) and the back (the node for the last value) for a double linked list. This simplifies the code dealing with insertion and removal of nodes. The dummy node for an empty list would have next and prev pointing to itself.

Another possible usage is for a single linked linear list where a dummy node inserted before the first node simplifies the code dealing with an empty list (no longer a special case).

Dummy node - location

If the dummy node is allocated on the heap there are two choices:

• ensure that list always have a dummy node, which leads to a potentially throwing default constructor and move constructor
• or introduce a special state, when default constructed or moved from, where there is no dummy node (this option partially negates the advantages of having a dummy node)

Alternatively the dummy node can be part of the header. This creates links from remote parts to local parts.

Permanent end iterator

The end iterator is one past the back. A permanent end iterator does not get invalidated as nodes get inserted or removed.

NOTE: Examples of permanent end iterator:

• a pointer to a dummy node
• a nullptr in a minimalistic iterator
• a non-minimalistic iterator containing a pointer to the header

ForwardIterator vs BidirectionalIterator

All list iterators are at least ForwardIterator.

Double linked lists iterators can be BidirectionalIterator. Not all double linked lists expose a BidirectionalIterator. Typically the problem is with moving backwards from the end iterator. For example if the end iterator is a just a nullptr pointer, it cannot implement the operator-- leading to a ForwardIterator only.

NOTE: there is a difference between the ability to traverse a sequence in the reverse orderer (back to front), which all double linked lists can have, and a BidirectionalIterator that requires the ability to change the direction of travel.

Intrusive vs. non-intrusive

For non-intrusive lists, the user of the list does not care about the layout of the node. They are easier to use.

For the intrusive lists, the user of the list has to be aware of the layout of the node. They know for a node the offsets for the value and pointer(s) to the adjacent nodes.

Intrusive lists are more difficult to use than non-intrusive lists, but have advantages. E.g. they allow for more explicit memory management, different exception safety guarantees, ability to have a node part of multiple lists/data structures.

Getting an iterator from a reference to a value

One possible facility is to provide a mean to get an iterator from a reference to a value. This is usually the case for intrusive lists, but can be provided for non-intrusive lists as well.

Node ownership

If the list owns the nodes, they get deleted when the list gets destroyed.

The other option is that the list does not own the nodes. This is usually the case with intrusive lists, in particular when a node is part of more than a list, at most one list can own the nodes.

Allocators

A variety of options can be made for how the nodes are allocated. Allocating nodes on the heap is usually the default option.

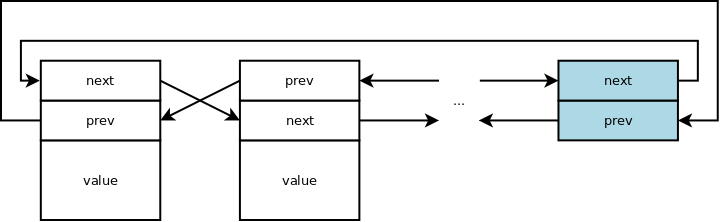
Meaning of pointers in the node

Most lists have fixed meaning for the pointers in the node (e.g. first is next, second is prev).

Fast reverse of double linked lists can be achieved if the meaning of next and prev is fixed just for the entry point in the list (e.g. the dummy node) while for the rest of the nodes it is deduced. This obviously has additional cost for other operations.

Thread safety

There is the option to use synchronization primitives such as compare-and-swap that support concurrent usage from multiple threads. Sometimes these are presented as lock-free lists, but bear in mind that lock-free does not mean synchronization-free, so the actual difference in performance compared with a list synchronized with locks needs to be measured, don’t assume the “free” one is faster.

Conclusion

The linked lists are one of the simplest data structures, and yet there is a large number of design options; some are totally independent, some are trade-offs.

References

Alexander A. Stepanov and Paul McJones:
Elements of Programming

Robert Endre Tarjan:
Data Structures and Network Algorithms