Finding the partition point for a partitioned range

Introduction

We’re going to have a look at a function similar to std::partition_point from the standard C++ library with some differences.

Here is a sample where the range has a partition point where we transition from vowels to consonants.

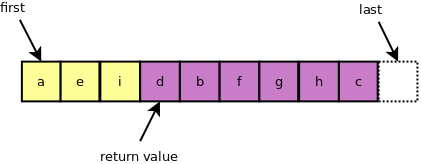
Partition point

See the article on min as to why we care.

A possible implementation looks like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

namespace algs {
  // generalized partition point for counted range taking predicate and projection
  template<typename I, typename N, typename Pred, typename Proj>
  // requires I is an ForwardIterator,
  //   N is a distance for I
  //   Pred is an unary predicate on projection Proj of ValueType(I)
  I partition_point_n(I f, N n, Pred pred, Proj proj) {
    while (n != 0) {
      N half = n / 2;
      I middle = std::next(f, half);
      if (pred(std::invoke(proj, *middle))) {
        n = half;
      }
      else {
        f = std::next(middle);
        n -= (half + 1);
      }
    }
    return f;
  }

  // generalized partition point taking predicate and projection
  template<typename I, typename S, typename Pred, typename Proj>
  // requires I is an ForwardIterator,
  //   S is a sentinel for I
  //   Pred is an unary predicate on projection Proj of ValueType(I)
  I partition_point(I f, S l, Pred pred, Proj proj) {
    auto n = std::distance(f, l);
    return partition_point_n(f, n, pred, proj);
  }

  // ... less general options implemented in terms of the above
}

The rest of the article is about how did we get there.

Basic usage

Basic usage of partition_point looks like this:

1
2
3
4
5
6
7
8
9
10
11
12

  std::vector<char> v{'a', 'e', 'i', 'd', 'b', 'f', 'g', 'h', 'c'};
  auto is_consonant = [](char x) {
    switch(x) {
      case 'a': case 'e': case 'i': case 'o': case 'u': return false;
      default: return true;
    }
  };
  auto pp = algs::range::partition_point(v, is_consonant);
  if (pp == v.end()) {
    std::cout << "FAIL!\n"; // we know we have consonants
  }
  std::cout << *pp << '\n'; // Prints d

How it works

This implementation is different from std::partition_point in that the range is partitioned so that the values for which the predicate returns false preceed the values for which the predicate returns true.

It turns out that implementing partition_point is just a wrapper for an algorithm that takes a counted range consisting of an iterator and a count: partition_point_n.

For partition_point_n we start with a counted range that we don’t know initially where is the partition point, and by halving at each step we determine on which side of the partition we are, and if we need to continue to the right or to the left.

Below is an example searching for the point where the range transitions from vowels to consonants. The return value is one past the last element in the the vowels range.

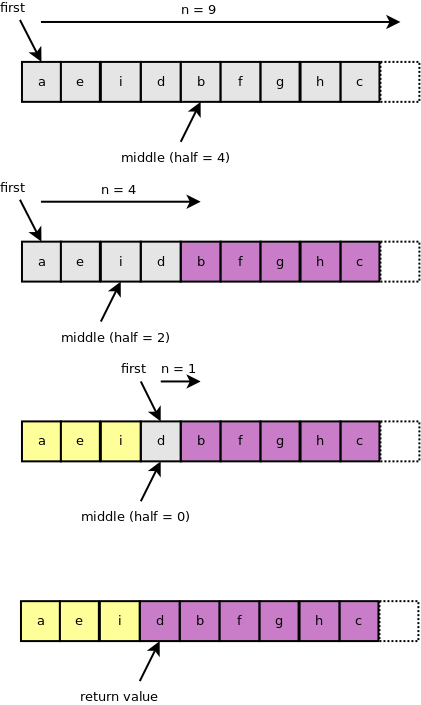
Partition point n

Algorithmic complexity

The function takes O(lg(n)) predicate applications in the worst case. Notice however that if the iterator is only ForwardIterator then calculating the distances degrades to O(n) steps. If the iterator is RandomAccessIterator distances between iterators can be calculated in constant time leading to O(lg(n)) time complexity. Using this algorithm for ForwarIterator is worthwhile only in some cases where predicate applications are much more expensive than traversals.

It is particularly suited for cases where the input is a sorted extent based (i.e. array-like) data structure, because it uses less memory and is cache friendly compared with node based data structures (i.e. linked lists, trees).

Related algorithms

  • partition, partition_semistable, stable_partition (partitioning a range)
  • lower_bound, upper_bound, equal_range (efficient find in sorted ranges)

References