Efficient find in a sorted range

Introduction

We’re going to have a look at a function similar to std::lower_bound from the standard C++ library with some differences.

The name lower_bound is easier to understand if we look at equal_range and upper_bound as well.

equal_range returns two iterators that define the range of a value in a sorted range (assuming a value can appear multiple times). lower_bound is just the first iterator, i.e. the beginning of the equal value range. upper_bound is the second iterator, i.e. the end of the equal value range, in a ‘one past the last’ sense.

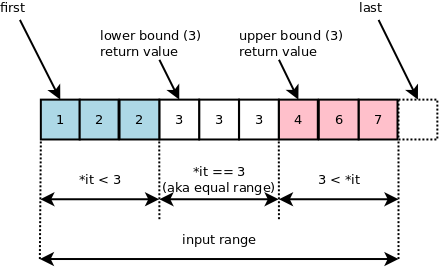
Lower bound

See the article on min as to why we care.

A possible implementation looks like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

namespace algs {
  namespace impl {
    template<typename T, typename Cmp>
    struct lower_bound_predicate {
      const T & value_;
      Cmp cmp_;

      lower_bound_predicate(const T & value, Cmp cmp)
        : value_{ value }, cmp_{ cmp } {
      }

      bool operator()(const T & at_it) {
        return !cmp_(at_it, value_);
      }
    };
  }

  // generalized lower_bound point taking comparison and projection
  template<typename I, typename S, typename T, typename Cmp, typename Proj>
  // requires I is an ForwardIterator,
  //   S is a setinel for I
  //   Cmp is a strict weak ordering on projection Proj of ValueType(I) and T
  I lower_bound(I f, S l, const T & value, Cmp cmp, Proj proj) {
    algs::impl::lower_bound_predicate<T, Cmp> pred{ value, cmp };
    return partition_point(f, l, pred, proj);
  }

  // ... less general options implemented in terms of the above
}

The rest of the article is about how did we get there.

Basic usage

Basic usage of lower_bound looks like this:

1
2
3
4
5

  std::vector<char> v{ 1, 2, 2, 3, 3, 3, 4, 6, 7 };
  auto it = algs::range::lower_bound(v, 3);
  if ((it == v.end()) || (*it != 3)) {
    std::cout << "FAIL!\n";
  }

How it works

This implementation is basically an application of std::partition_point, with a suitably defined predicate: lower_bound_predicate.

lower_bound_predicate is chosen such that *it < value is false.

The constructor or lower_bound_predicate captures the value and comparison to use. One tiny unusual fact is that the value is captured in a const & member, so we need to ensure that the scope of value is larger than the scope of the lower_bound_predicate instance.

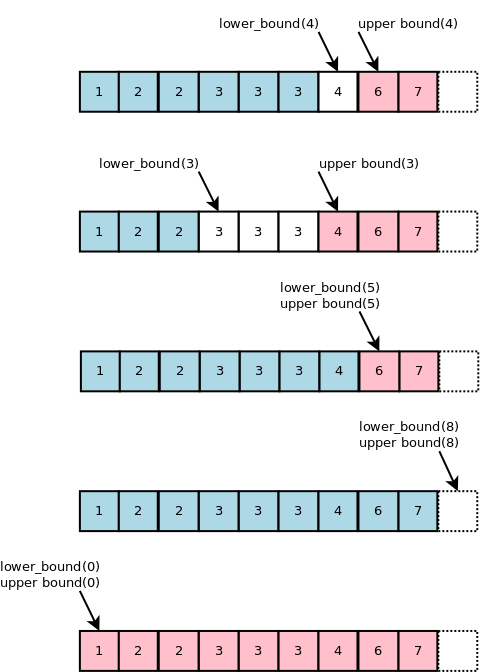
Below are example return values for various scenarios.

Lower bound_samples

Algorithmic complexity

Is the same as for partition_point: O(lg(n)) (except for ForwardIterator only where it could still be useful sometimes).

Non-homogeneous predicate

The comparison predicate used by lower_bound does not have to have the same type for both arguments, i.e. it does not have to be homogeneous. The first argument is related to the value_type of the iterators, while the second argument is related to the type T, and sometimes these types are different.

For example one can look and find a contact by name like this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

  struct contact {
    std::string name;
    std::string email;
  };

  std::vector<contact>::const_iterator
  find_contact_by_name(const std::vector<contact> & contacts, const std::string & name) {

    // Comparison lambda has different argument types.
    // It compares a contact with a string.
    // This avoids having to construct a temporary contact
    // just so that we can compare two contact objects
    auto comp = [](const contact & c, const std::string & name) {
      return c.name < name;
    };

    auto it = algs::range::lower_bound(contacts, name, comp);
    if (it == contacts.end()) {
      return it;
    }
    if (it->name != name) {
      return contacts.end();
    }
    return it;
  }

  void some_fn() {
    // ...
    auto it = find_contact_by_name(my_contacts, some_name);
    if (it != my_contacts.end()) {
      std::cout << "Found email: " << it->email << '\n';
    }
    // ...
  }

This is similar to the discussion we had on the linear find article.

I’ve employed some of this idea in a complex case where syntactically the comparison was homogeneous (it compared file system paths), but semantically it was not, because the container contains a mixture of folder and file paths, while the value provided was a full file path, trying to determine if it’s matches either a full file path on the container or it is in a folder path stored in the container.

Related algorithms

  • partition_point, partition_point_n (finding using predicate)
  • upper_bound (finding the end of a value range)
  • equal_range (combines lower_bound and upper_bound)
  • binary_search (returns true if value is found: it’s lower bound with an extra check for the value)
  • sort, stable_sort (sort range to allow efficient search)

Conclusion

This series of articles started with min, find and swap and claimed that they are fundamental programming blocks, that a programming language needs to get right. Then we looked at partion without being instantly clear as to where it is useful.

Now we got to lower_bound which, despite it’s maybe unusual name, is the first obviously useful generic function: efficiently (logarithmic and cache friendly) finding values in a partitioned/sorted range.

References